what is [cr3+] when [ni2+] has dropped to 10-4 m?

Chapter 17. Electrochemistry

17.4 The Nernst Equation

Learning Objectives

Past the stop of this section, yous will be able to:

• Relate cell potentials to free free energy changes
• Use the Nernst equation to decide cell potentials at nonstandard atmospheric condition
• Perform calculations that involve converting between jail cell potentials, free free energy changes, and equilibrium constants

We volition now extend electrochemistry by determining the human relationship betwixt [latex]E_{\text{cell}}^{\circ}[/latex] and the thermodynamics quantities such as ΔG° (Gibbs complimentary energy) and M (the equilibrium constant). In galvanic cells, chemic energy is converted into electrical energy, which can practise work. The electric work is the product of the accuse transferred multiplied by the potential difference (voltage):

[latex]\text{electric\;work} = \text{volts}\;\times\;(\text{charge\;in\;coulombs}) = \text{J}[/latex]

The charge on 1 mole of electrons is given by Faraday's constant (F)

[latex]F = \frac{half-dozen.022\;\times\;ten^{23}\text{e}^{-}}{mol}\;\times\;\frac{1.602\;\times\;ten^{-nineteen}\;\text{C}}{\text{e}^{-}} = 9.648\;\times\;10^{four}\;\frac{\text{C}}{\text{mol}} = ix.684\;\times\;10^{4}\frac{\text{J}}{\text{5}{\cdot}\text{mol}}[/latex]

[latex]\text{total\;charge} = (\text{number\;of\;moles\;of\;eastward}^{-})\;\times\;F = nF[/latex]

In this equation, n is the number of moles of electrons for the balanced oxidation-reduction reaction. The measured cell potential is the maximum potential the prison cell can produce and is related to the electric work (due west _ele) by

[latex]E_\text{jail cell} = \frac{-w_{\text{ele}}}{nF}\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;w_{\text{ele}} = -nFE_{\text{cell}}[/latex]

The negative sign for the work indicates that the electrical work is washed past the arrangement (the galvanic jail cell) on the environs. In an earlier chapter, the free energy was divers as the energy that was available to practise work. In particular, the alter in free energy was divers in terms of the maximum work (w _max), which, for electrochemical systems, is w _ele.

[latex]{\Delta}1000 = w_{\text{max}} = w_{\text{ele}}[/latex]

[latex]{\Delta}G = -nFE_{\text{cell}}[/latex]

We can verify the signs are right when nosotros realize that n and F are positive constants and that galvanic cells, which accept positive jail cell potentials, involve spontaneous reactions. Thus, spontaneous reactions, which have ΔG < 0, must have E _cell > 0. If all the reactants and products are in their standard states, this becomes

[latex]{\Delta}G^{\circ} = -nFE_{\text{cell}}^{\circ}[/latex]

This provides a way to relate standard cell potentials to equilibrium constants, since

[latex]{\Delta}Grand^{\circ} = -RT\;\text{ln}\;Thousand[/latex]

[latex]-nFE_{\text{jail cell}}^{\circ} = -RT\;\text{ln}\;G\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;E_{\text{cell}}^{\circ} = \frac{RT}{nF}\;\text{ln}\;K[/latex]

Most of the time, the electrochemical reactions are run at standard temperature (298.xv Grand). Collecting terms at this temperature yields

[latex]E_{\text{jail cell}}^{\circ} = \frac{RT}{nF}\;\text{ln}\;K = \frac{(eight.314\frac{\text{J}}{\text{K}{\cdot}\text{mol}})(298.15K)}{n\;\times\;96,485\;\text{C/5}{\cdot}\text{mol}}\;\text{ln}\;Grand = \frac{0.0257\;\text{V}}{n}\;\text{ln}\;M[/latex]

where n is the number of moles of electrons. For historical reasons, the logarithm in equations involving cell potentials is ofttimes expressed using base ten logarithms (log), which changes the constant by a factor of 2.303:

[latex]E_{\text{prison cell}}^{\circ} = \frac{0.0592\;\text{5}}{northward}\;\text{log}\;1000[/latex]

Thus, if ΔG°, K, or [latex]E_{\text{cell}}^{\circ}[/latex] is known or tin be calculated, the other two quantities can be readily determined. The relationships are shown graphically in Effigy one.

Figure 1. The relationships between Δ1000 ^°, K, and E ^° _{prison cell}. Given whatsoever one of the iii quantities, the other two tin can be calculated, then whatsoever of the quantities could be used to decide whether a process was spontaneous.

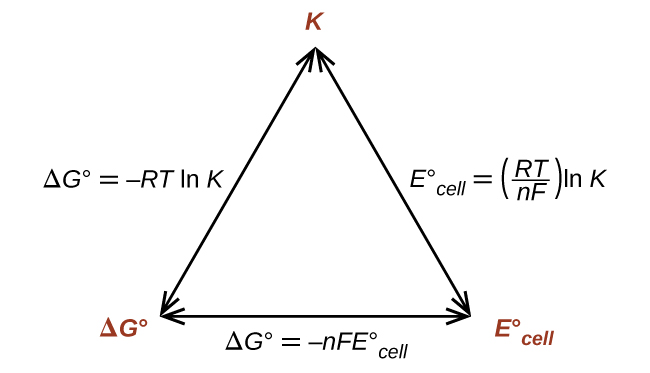
Given whatever one of the quantities, the other 2 can exist calculated.

Instance i

Equilibrium Constants, Standard Cell Potentials, and Standard Costless Energy Changes
What is the standard free energy change and equilibrium constant for the following reaction at 25 °C?

[latex]two\text{Ag}^{+}(aq)\;+\;\text{Atomic number 26}(southward)\;{\leftrightharpoons}\;two\text{Ag}(s)\;+\;\text{Fe}^{2+}(aq)[/latex]

Solution
The reaction involves an oxidation-reduction reaction, so the standard cell potential can be calculated using the data in Appendix L.

[latex]\begin{array}{lr @{{}\longrightarrow{}} ll} \text{anode\;(oxidation):} & \text{Fe}(s) & \text{Fe}^{2+}(aq)\;+\;2\text{e}^{-} & E_{\text{Atomic number 26}^{2+}/\text{Fe}}^{\circ} = -0.447\;\text{V} \\[0.5em] \text{cathode\;(reduction):} & 2\;\times\;(\text{Ag}^{+}(aq)\;+\;\text{eastward}^{-} & \text{Ag}(due south)) & E_{\text{Ag}^{+}/\text{Ag}}^{\circ} = 0.7996;\text{V} \finish{array}[/latex]

[latex]E_{\text{cell}}^{\circ} = E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} = E_{\text{Ag}^{+}/\text{Ag}}^{\circ}\;-\;E_{\text{Fe}^{two+}/\text{Atomic number 26}}^{\circ} = +1.247\;\text{V}[/latex]

Call back that the cell potential for the cathode is not multiplied by ii when determining the standard cell potential. With n = 2, the equilibrium constant is so

[latex]E_{cell}^{\circ} = \frac{0.0592\;\text{V}}{n}\;\text{log}\;K[/latex]

[latex]K = 10^{n\;\times\;E_{\text{cell}}^{\circ}/0.0592\;\text{5}}[/latex]

[latex]Chiliad = 10^{2\;\times\;1.247\;\text{5}/0.0592\;\text{V}}[/latex]

[latex]K = ten^{42.128}[/latex]

[latex]M = 1.3\;\times\;10^{42}[/latex]

The two equilibrium constants differ slightly due to rounding in the constants 0.0257 V and 0.0592 V. The standard complimentary energy is and then

[latex]{\Delta}G^{\circ} = -nFE_{\text{jail cell}}^{\circ}[/latex]

[latex]{\Delta}Thousand^{\circ} = -two\;\times\;96,485\;\frac{\text{J}}{\text{V}{\cdot}\text{mol}}\;\times\;one.247\;\text{V} = -240.6\;\frac{\text{kJ}}{\text{mol}}[/latex]

Bank check your answer: A positive standard prison cell potential means a spontaneous reaction, then the standard costless energy change should be negative, and an equilibrium abiding should be >1.

Bank check Your Learning
What is the standard free energy change and the equilibrium abiding for the following reaction at room temperature? Is the reaction spontaneous?

[latex]\text{Sn}(s)\;+\;2\text{Cu}^{ii+}(aq)\;{\leftrightharpoons}\;\text{Sn}^{two+}(aq)\;+\;2\text{Cu}^{+}(aq)[/latex]

Answer:

Spontaneous; n = 2; [latex]E_{\text{jail cell}}^{\circ} = +0.291\;\text{Five;}\;{\Delta}K^{\circ} = -56.ii\;\frac{\text{kJ}}{\text{mol}}[/latex]; K = 6.8 × 10⁹.

Now that the connectedness has been made between the energy and cell potentials, nonstandard concentrations follow. Call up that

[latex]{\Delta}1000 = {\Delta}Grand^{\circ}\;+\;RT\;\text{ln}\;Q[/latex]

where Q is the reaction caliber (see the chapter on equilibrium fundamentals). Converting to jail cell potentials:

[latex]-nFE_{\text{prison cell}} = -nFE_{\text{cell}}^{\circ}\;+\;RT\;\text{ln}\;Q\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{RT}{nF}\;\text{ln}\;Q[/latex]

This is the Nernst equation. At standard temperature (298.15 K), it is possible to write the above equations as

[latex]E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{0.0257\;\text{V}}{n}\;\text{ln}\;Q\;\;\;\;\;\;\;\text{or}\;\;\;\;\;\;\;E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{0.0592\;\text{V}}{northward}\;\text{log}\;Q[/latex]

If the temperature is not 273.15 Yard, it is necessary to recalculate the value of the constant. With the Nernst equation, information technology is possible to calculate the cell potential at nonstandard conditions. This adjustment is necessary because potentials determined under different conditions will take unlike values.

Example 2

Cell Potentials at Nonstandard Weather condition
Consider the following reaction at room temperature:

[latex]\text{Co}(s)\;+\;\text{Atomic number 26}^{2+}(aq\text{,\;}1.94\;Chiliad)\;{\longrightarrow}\;\text{Co}^{2+}(aq\text{,\;}0.fifteen\;Yard)\;+\;\text{Atomic number 26}(due south)[/latex]

Is the process spontaneous?

Solution
There are two ways to solve the trouble. If the thermodynamic data in Appendix Chiliad were available, you could calculate the gratis energy change. If the free energy modify is negative, the process is spontaneous. The other approach, which nosotros volition use, requires information like that given in Appendix L. Using those data, the cell potential can be determined. If the cell potential is positive, the procedure is spontaneous. Collecting data from Appendix Fifty and the problem,

[latex]\begin{array}{lr @{{}\longrightarrow{}} ll} \text{Anode\;(oxidation):} & \text{Co}(s) & \text{Co}^{2+}(aq)\;+\;2\text{e}^{-} & E_{\text{Co}^{2+}/\text{Co}}^{\circ} = -0.28\;\text{V} \\[0.5em] \text{Cathode\;(reduction):} & \text{Fe}^{2+}(aq)\;+\;2\text{e}^{-} & \text{Fe}(due south) & E_{\text{Atomic number 26}^{2+}/\text{Fe}}^{\circ} = -0.447\;\text{Five} \end{array}[/latex]
[latex]E_{\text{cell}}^{\circ} = E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} = -0.447\;\text{V}\;-\;(-0.28\;\text{Five}) = -0.17\;\text{5}[/latex]

The process is not spontaneous nether standard weather condition. Using the Nernst equation and the concentrations stated in the problem and n = 2,

[latex]Q = \frac{[\text{Co}^{2+}]}{[\text{Fe}^{two+}]} = \frac{0.15\;1000}{i.94\;Grand} = 0.077[/latex]

[latex]E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{0.0592\;\text{V}}{n}\;\text{log}\;Q[/latex]

[latex]E_{\text{cell}} = -0.17\;\text{V}\;-\;\frac{0.0592\;\text{V}}{2}\;\text{log}\;0.077[/latex]

[latex]E_{\text{cell}} = -0.17\;\text{V}\;+\;0.033\;\text{V} = -0.014\;\text{V}[/latex]

The process is (nonetheless) nonspontaneous.

Bank check Your Learning
What is the cell potential for the following reaction at room temperature?

[latex]\text{Al}(s){\mid}\text{Al}^{three+}(aq\text{,\;}0.xv\;Chiliad){\parallel}\text{Cu}^{2+}(aq\text{,\;}0.025\;M){\mid}\text{Cu}(s)[/latex]

What are the values of n and Q for the overall reaction? Is the reaction spontaneous under these conditions?

Answer:

n = 6; Q = 1440; E _cell = +1.97 V, spontaneous.

Finally, nosotros will take a brief await at a special type of cell called a concentration jail cell. In a concentration cell, the electrodes are the same material and the half-cells differ only in concentration. Since i or both compartments is not standard, the cell potentials will be unequal; therefore, in that location will be a potential divergence, which tin can be adamant with the aid of the Nernst equation.

Case 3

Concentration Cells
What is the jail cell potential of the concentration prison cell described past

[latex]\text{Zn}(south){\mid}\text{Zn}^{2+}(aq\text{,\;}0.10\;M){\parallel}\text{Zn}^{two+}(aq\text{,\;}0.50\;Chiliad){\mid}\text{Zn}(s)[/latex]

Solution
From the information given:

[latex]\begin{assortment}{lr @{{}\longrightarrow{}} ll} \text{Anode:} & \text{Zn}(s) & \text{Zn}^{ii+}(aq\text{,\;}0.10\;M)\;+\;2\text{e}^{-} & E_{\text{anode}}^{\circ} = -0.7618\;\text{5} \\[0.5em] \text{Cathode:} & \text{Zn}^{ii+}(aq\text{,\;}0.50\;M)\;+\;ii\text{e}^{-} & \text{Zn}(s) & E_{\text{cathode}}^{\circ} = -0.7618\;\text{5} \\[0.5em] \hline \\[-0.25em] \text{Overall:} & \text{Zn}^{ii+}(aq\text{,\;}0.50\;M) & \text{Zn}^{two+}(aq\text{,\;}0.10\;1000) & E_{\text{prison cell}}^{\circ} = 0.000\;\text{V} \stop{assortment}[/latex]

The standard cell potential is zero because the anode and cathode involve the same reaction; only the concentration of Zn²⁺ changes. Substituting into the Nernst equation,

[latex]E_{\text{jail cell}} = 0.000\;\text{V}\;-\;\frac{0.0592\;\text{V}}{2}\;\text{log}\;\frac{0.10}{0.50} = +0.021\;\text{5}[/latex]

and the process is spontaneous at these conditions.

Bank check your answer: In a concentration cell, the standard jail cell potential will always be cipher. To get a positive cell potential (spontaneous process) the reaction quotient Q must exist <1. Q < one in this instance, and then the process is spontaneous.

Check Your Learning
What value of Q for the previous concentration cell would result in a voltage of 0.10 V? If the concentration of zinc ion at the cathode was 0.50 M, what was the concentration at the anode?

Answer:

Q = 0.00042; [Zn²⁺]_cat = 2.1 × x⁻⁴ M.

Key Concepts and Summary

Electric work (due west _ele) is the negative of the product of the total charge (Q) and the jail cell potential (E _{jail cell}). The total charge tin be calculated as the number of moles of electrons (n) times the Faraday constant (F = 96,485 C/mol e⁻). Electric piece of work is the maximum work that the system can produce and and then is equal to the change in costless free energy. Thus, annihilation that can be done with or to a gratuitous energy change tin can also be washed to or with a cell potential. The Nernst equation relates the prison cell potential at nonstandard weather to the logarithm of the reaction quotient. Concentration cells exploit this relationship and produce a positive cell potential using half-cells that differ only in the concentration of their solutes.

Central Equations

• [latex]E_{\text{cell}}^{\circ} = \frac{RT}{nF}\;\text{ln}\;K[/latex]
• [latex]E_{\text{cell}}^{\circ} = \frac{0.0257\;\text{V}}{northward}\;\text{ln}\;Chiliad = \frac{0.0592\;\text{V}}{n}\;\text{log}\;K\;\;\;\;\;\;\;(\text{at}\;298.15\;Yard)[/latex]
• [latex]E_{\text{cell}} = E_{\text{jail cell}}^{\circ}\;-\;\frac{RT}{nF}\;\text{ln}\;Q\;\;\;\;\;\;\;(\text{Nernst equation})[/latex]
• [latex]E_{\text{jail cell}} = E_{\text{cell}}^{\circ}\;-\;\frac{0.0257\;\text{V}}{northward}\;\text{ln}\;Q = \frac{0.0592\;\text{Five}}{n}\;\text{log}\;Q\;\;\;\;\;\;\;(\text{at}\;298.fifteen\;Grand)[/latex]
• [latex]{\Delta}Chiliad = -nFE_{\text{cell}}[/latex]
• [latex]{\Delta}Yard^{\circ} = -nFE_{\text{prison cell}}^{\circ}[/latex]
• [latex]w_{\text{ele}} = w_{\text{max}} = -nFE_{\text{cell}}[/latex]

Chemistry End of Affiliate Exercises

1. For the standard jail cell potentials given here, make up one's mind the ΔG° for the cell in kJ.

   (a) 0.000 Five, n = two

   (b) +0.434 V, n = 2

   (c) −2.439 V, due north = one

2. For the ΔThousand° values given hither, make up one's mind the standard cell potential for the cell.

   (a) 12 kJ/mol, n = 3

   (b) −45 kJ/mol, n = 1

3. Decide the standard cell potential and the cell potential under the stated conditions for the electrochemical reactions described here. Land whether each is spontaneous or nonspontaneous under each set of conditions at 298.fifteen M.

   (a) [latex]\text{Hg}(fifty)\;+\;\text{Due south}^{2-}(aq\text{,\;}0.10\;M)\;+\;two\text{Ag}^{+}(aq\text{,\;}0.25\;M)\;{\longrightarrow}\;two\text{Ag}(s)\;+\;\text{HgS}(s)[/latex]

   (b) The galvanic cell made from a half-cell consisting of an aluminum electrode in 0.015 M aluminum nitrate solution and a half-cell consisting of a nickel electrode in 0.25 Thou nickel(II) nitrate solution.

   (c) The cell made of a half-cell in which 1.0 M aqueous bromine is oxidized to 0.11 M bromide ion and a half-jail cell in which aluminum ion at 0.023 M is reduced to aluminum metal. Presume the standard reduction potential for Br_two(l) is the same as that of Br_ii(aq).

4. Make up one's mind ΔYard and ΔThou° for each of the reactions in the previous problem.
5. Utilise the data in Appendix Fifty to decide the equilibrium constant for the post-obit reactions. Assume 298.fifteen 1000 if no temperature is given.

   (a) [latex]\text{AgCl}(s)\;{\leftrightharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)[/latex]

   (b) [latex]\text{CdS}(s)\;{\leftrightharpoons}\;\text{Cd}^{2+}(aq)\;+\;\text{S}^{2-}(aq)\;\;\;\;\;\;\;\text{at}\;377\;\text{K}[/latex]

   (c) [latex]\text{Hg}^{2+}(aq)\;+\;4\text{Br}^{-}(aq)\;{\leftrightharpoons}\;[\text{HgBr}_4]^{2-}(aq)[/latex]

   (d) [latex]\text{H}_2\text{O}(50)\;{\leftrightharpoons}\;\text{H}^{+}(aq)\;+\;\text{OH}^{-}(aq)\;\;\;\;\;\;\;\text{at}\;25^{\circ}\;\text{C}[/latex]

Glossary

concentration cell

galvanic cell in which the two half-cells are the aforementioned except for the concentration of the solutes; spontaneous when the overall reaction is the dilution of the solute

electrical work (w _ele)

negative of total charge times the cell potential; equal to westward _max for the system, so equals the complimentary energy alter (ΔYard)

Faraday's constant (F)

charge on i mol of electrons; F = 96,485 C/mol e⁻

Nernst equation

equation that relates the logarithm of the reaction quotient (Q) to nonstandard cell potentials; can be used to relate equilibrium constants to standard prison cell potentials

Solutions

Answers to Chemistry Cease of Chapter Exercises

1. (a) 0 kJ/mol; (b) −83.7 kJ/mol; (c) +235.3 kJ/mol

3. (a) standard cell potential: 1.50 V, spontaneous; prison cell potential under stated weather: 1.43 Five, spontaneous; (b) standard cell potential: 1.405 V, spontaneous; cell potential under stated weather condition: one.423 Five, spontaneous; (c) standard cell potential: −2.749 Five, nonspontaneous; prison cell potential under stated weather: −2.757 V, nonspontaneous

5. (a) 1.7 × 10^−ten; (b) two.6 × 10⁻²¹; (c) eight.9 × 10¹⁹; (d) ane.0 × 10^−xiv

hicksonbaid1970.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/17-4-the-nernst-equation/

Share this post